Nx Ue E Ss
0513 · x n − y n = (x − y) ∑ i = 1 n x n − i y i − 1 x^{n}y^{n} = (xy)\sum_{i=1}^{n}x^{ni}y^{i1} x n − y n = (x − y) ∑ i = 1 n x n − i y i − 1 Bashar schrieb Ich verstehe irgendwie den Sinn der Aufgabe nicht ganz So geht mir das auch bei manchen.

Nx ue e ss. · wir verzweifeln gerade daran, den Grenzwert der Folge bn=(x^ny^n)^(1/n) (x,y>0, n Element von N) zu bestimmen Hat jemand eine Idee für einen Ansatz?. · Hallöchen Ich habe hier noch diese Aufgabe zu lösen Berechnen Sie den Grenzwert der Folge für n>\inf und zeigen Sie dann, dass sie konvergent ist a_n = x^n/n!. ß ¯ BV QBJST 3 î È ) L ß À ² à È N z ( R 8 b ü à È \ I d W ¹ I ) L À S î î ½ ã é ç 7 ' N z W \ ý N z è I J < x é Ñ F 7 û > ) L ý \ ¯ ó î È ½ ã é ç ± ý û S × (D I ¹ 7 d é Ò Ò Ï } > · · Þ î Ò = X ò è I ¹ Â > ä è 8 > ç û K d D I ¹ I Ý x 5 ý > Þ ç.
Ò Ê Ø á Ð Ý Ó Ð å �. Lineare Algebra DMATH, HS 14 Prof Richard Pink L osung zu Serie 13 1 Aufgabe Seien V ein KVektorraum und F;G2End(V) Zeige a) Falls v2V ein Eigenvektor von F. N= {(x 1,,x n) x i ∈ M i f¨ur i = 1,,n} F¨ur das nfache kartesische Produkt einer Menge M benutzen wir auch die Notation Mn Mn= M ×···×M {z } n−mal = {(x 1,,x n) x i ∈ M f¨ur i = 1,,n} Ein Element (x,y) ∈ M ×N bezeichnen wir auch als ein (geordnetes) Paar und ein Element (x 1,,x n) ∈ M 1 ×···×M n wird oft (geordnetes).
= 3 1 1 1 4 1 = 3 (c) X1 n=0 ( 3)n 4n = X1 n=0 ( 1)n 3 4 n = (analogzua) = 4 7 (d) Zuerst betrachtet man 1 4n2 1 = 1 (2n1)(2n 1) = 1 2 2n1 1 2 2n 1 Damit ist die nte Partialsumme (Teleskopsumme) s n= 1 2 1 1 1 3 1 3 1 5 1 2n1 = 1 2 1 1 2n1 !1 2 9 Konvergenzradien von. / \ *¡à !¡ 1 " / !. Eine Funktion f mit einer Gleichung der Form y = f ( x ) = m x n ( m , n ∈ ℝ ) oder einer Gleichung, die durch äquivalentes Umformen in diese Form überführt werden kann, heißt lineare FunktionFür lineare Funktionen ist der Definitionsbereich im Allgemeinen die Menge der reellen Zahlen (so nicht das mathematische oder das entsprechenden Anwendungsproblem einen.
G ¡ 2 !. ´ 2 Ý È } d (·················································································· ´ )fscfsh d 2 Ý È. 2 KAPITEL I GRUNDLAGEN Abbildungen Es seien Mengen X und Y gegeben Eine Abbildung (oder Funktion) von X nach Y besteht aus X und Y zusammenmiteinerTeilmengefvonX Y so,dassesfürjedesx2Xgenaueiny2Y mit(x;y) 2fgibt.
NX1 k=0 n1 k = nX1 k=0 n k n k 1 = k=0 n k nX1 k=1 n k 1 = 2n2n= 2n1 (vi)BeweisedieBernoulliUngleichung(1x)n>1nxfürn 2 undx> 1;x6= 0 Beweis (IA) n= 2 (1x) 2= 12xx >12x Beachte das x6= 0 gilt (IS) n7!n1 (1x)n1 = (1x)(1x)n>(1x)(1nx) = 1xnxnx2 >1(n1)x (vii)ZeigefolgendeRelationen (1) n!. 1 Gruppenubung¨ H¨ohere Mathematik 2 Uberpr¨ ¨ufen Sie, ob die Folge konvergiert und bestimmen Sie gegeben enfalls ihren Grenzwert L¨osungshinweise hierzu Wir bestimmen zun¨achst den m ¨oglichen Grenzwert der Folge und. Wenn f(n)(x) = (x n)ex richtig ist, dann folgt f(n1)(x) = (f(n)(x))0= ((x n)ex)0 = e x (x n)ex = ex xe x ne = (x n 1)e ;.
Sn = k=1 (k √ 25− k1 √ 25) = (1 √ 25− 2 √ 25)(2 √ 25− 3 √ 25)(3 √ 25− 4 √ 25)···(n √ 25− n1 √ 25) = 1 √ 25− n1 √ 25 = 25− n1 √ 25, daher gilt X∞ n=1 (n √ 25− n1 √ 25) = lim n→∞ Sn = 25−1 = 24 (vgl Beispiel 157) (c) Diese Reihe l¨asst sich durch Indexverschiebung auf die Exponentialreih e zur¨uckf ¨uhren (mit l = k 1) X∞ k=1 1. Für x\el\IR beliebig Zuerst die Berechnung des Grenzwerts Ich habe nun versucht, diese Folge umzuformen, jedoch ohne Erfolg Es ist lim(x>\inf,x^n/n!)=lim(x>\inf,x^n)/lim(x>\inf,n!) aber das bringt mich auch. ¹ B>ß>Ü º>&>Þ>Ü>Ý>ä º>'>2 v _ > 8 Z / d ¦ p b ² Ò'¼ b È2( ;6ä$Î 0¿ c ² \ >Þ>á 0¿ 6 ~ Q b0£#ì6ä$Î È5 c4 w#Ý È(Ù>7 h Q> º 3° #Ý È(Ù>/ h Q> º O Z(Ù>Ý>Ü h Q> º \ ^ W Z 8 >& \ u º3û%, È2( ;.
>, ¼ ( É ß Ç î Ý è c>* Ä º b _ ·>* ¼ (>* ¤ _ ^ 2A e(ì _ ~!l X ì M G \ @ A 0Û o { Ø 6 >, æ d ' & < c>* °/ 'ö(Ô b # b"g  /² K Z 8 >& Ó °*L15 ¡>*0è/ 6 1 *L15 ¡>' _ (8® K S>, Ó è c>* ° ¿ · Í>* X ¸ « º>* "(ç o  ì6ë @ w _ 5 K>* ¼ ( É ß Ç S>, Ó } _ 8 Z>* Ó ° K Z v } < G \ ó ° K Z q · _ v ~) u S G \ _ ~>* q · _ P M )m G x Y ó c3M ö. } x t N v È K Z 8 G \ @ 6 G b ^ v È c È @1Ï ) ^ \ A. Lösungsvorschläge zu ausgewählten Übungsaufgaben aus Storch/Wiebe Lehrbuch der Mathematik Band1, 3Aufl (Version 10), Kapitel 5 13 Differenzierbare Funktionen.
1 Bernstein, S,Leçons sur les propriétés extrémales et la meilleure approximation des fonctions analytiques d'une variable réelle (GauthierVillars, Paris 1926) Google Scholar 2 Fox, L and Parker, I B,Chebyshev Polynomials in Numerical Analysis (Oxford Univ Press, London, 1968) Google Scholar 3 Meinardus, G,Approximation von Funktionene und ihre numerische. Title Microsoft Word AfSdoc Author kasuchm Created Date 5/14/ AM. N (x y)j= jx n x (y n y)j jx n xj j (y n y)j 2 2 = Die Aussagen c) { e) lassen sich mit ahnlichen (etwas aufwendigeren) Absch atzungen beweisen QED Beispiel 214 Wir wissen bereits, dass konstante Folgen x n= cgegen ckonvergieren, und dass x n= 1 n eine Nullfolge ist Durch Einsatz der Rechenregeln folgt unmittelbar lim n!1 1 n2 = lim n!1 1 n 1 n = lim n!1 1 n lim n!1 1 n = 0 0 = 0.
N(x) Reiner Lauterbach (Mathematik, UniHH) Analysis I f ur Ingenieure 123 / 190 Stetige Funktionen De nition Sei f D !W;D ˆV eine Funktion 1)Die Funktion f (x) heiˇtstetig erg anzbar in x 0 2D0, falls lim x!x0 f (x) existiert und endlich ist 2)Die Funktion f (x) heiˇtstetig in x 0 2D \D0, falls lim x!x0 f (x) = f (x 0) gilt 3)Die Funktion f (x) heiˇtstetig, falls f (x. Warum sollte dieser Ausdruck \(=e\) sein?. Pr¨asenzAufgaben 1 Man bestimme alle Eigenr¨aume f ur die Matrix¨ A ∈ M(4× 4,F2) 1 1 0 0 0 1 1 0 0 0 1 1 1 0 0 1 2 Sei n ≥ 1 Sei A = (aij) eine (n× n.
4 1* m>' >Ì ® C Ò 7 þ È v È M È2( ;6ä$Î 0¿ @ r T ö B K Z 8 ^ 8"g # v Q b)m ô ö'¼ ?. ß L} û L % K A Study of GISbased Estimation of Pollutant Loads in Accordance with Spatial Landuse Variation Focussing on Wangsook Watershed KyoungSoon Kim*hKyeHyun Kim**hOhJun Kwon*** Greentech Environmental Consulting Co, Ltd. Ú ð v y ¡ Ù u y 0 W , v a à D ê ¿ É ñ %81 U ~ j z è ñ y ö ê ¿ É ñ y l e ¼ r y Ï ¤ Ú Q W Z r å r * D j z K × W ß.
N xn = 0, das Supremum existiert nicht 2 βVersion 509 GHR Analysis Kaßmann Nach der Definition ist es offensichtlich, dass eine Folge h¨ochstens ein Supremum bzw Infimum haben kann Dass nach oben beschr¨ankte Folgen immer ein Supremum haben (und nach unten beschr¨ankte Folgen immer ein Infimum), ist eine fundamentale Eigensc haft der reellen Zahlen. Atom/Quantenmechanik Prof Dr Andreas Görling Institut für Physikalische und Theoretische Chemie Friedrich–Alexander–Universität Erlangen–Nürnberg. Xn < y n mit einem passenden n ∈ N (nach Archimedes gibt es stets ein n > x) 1 Nachweis der Existenz eines ξ ∈ Q (Q ist die Menge der rationalen Zahlen) Nach Satz 45 gibt es ein n ∈ N mit 1 n < y−x (∗) Der Satz von Archimedes sichert die Existenz eines k ∈ N mit k ≥ ny, also k n ≥ y (†) Sei k 0 das kleinste solche k Wegen (∗) gilt k.
ß K Þ ß ® Ñ ;. 2 i / !. 2n 1 fürn>1;n2N Beweis (IA) n= 2 2!.
· Ueberlege Dir mit dem Hinweis zur Stetigkeit von exp und ln, dass das stimmt Verifiziere dann die rechte Formel Das geht einfacher , 1745 Merter Auf diesen Beitrag antworten » RE Zeigen das exp^x= lim (1x/n)^n Ich könnte ja die n reinmultiplizieren dann würde ja stehen lim ln ( (1x/n)^n ) = x. I ¿ ± ± ß ® ¸ & ß y p j tvohkpp!bkpv bd ls. Eine Funktion f mit einer Gleichung der Form y = f ( x ) = m x n ( m , n ∈ ℝ ) oder einer Gleichung, die durch äquivalentes Umformen in diese Form überführt werden kann, heißt lineare FunktionFür lineare Funktionen ist der Definitionsbereich im Allgemeinen die Menge der reellen Zahlen (so nicht das mathematische oder das entsprechenden Anwendungsproblem einen.
Satz 845 Sei Y !R eine Zufallsvariable mit EY. 2 \ã¡ 0 !. Lineare Algebra 2 Prof Dr R Dahlhaus Dr S Richter, N Phandoidaen Sommersemester 19 4 Abgabeblatt – L¨osungen Aufgabe 13 Aufgabe 14 Aufgabe 15 Aufgabe 16 Summe.
>ß È >ß5 ° Õ ¥>ß v æ >ß È gtgggv>ß u>ß º ²)glg g=>ß!f >ß >ø >ß ¥ e ìfþ ¥ >Þ º4 %Ê0°3Ù >ß º%31¤ 0è >ß!f>Ý>Ø>ß º gtgggv>ß5 >ß v>ÿ>Ì>Ý>Ø>Þ º>ß!f Û º gtgggv 4e ¤ =. N(n−2)α(n)x 2−n, n≥ 3, wobei α(n) = voln(B(0,1)) = π n/2 Γ(1n/2) das Volumen der ndimensionalen Einheitskugel ist, heißt Fundamentall¨osung f ¨ur die LaplaceGleichung Bemerkung 214 Tats¨achlich ist Φ eine L ¨osung der LaplaceGleichung auf Rn \{0}, wie man mittels Gleichung (21) leicht verifiziert 1(Rn)), aber. Â ä Ü Ñ Ô á Þ Õ â ã á Ø Ý Ö â Ø Ý È Ð Ý ß ä á Ð Ð Ñ Ò Ó í ó X !.
*¡ ¡ 0 × !. Ð µ Ú Ñ Ð á Ó Ç Ð è Ð Ù Ø Æ Ð Þ í ô X !. 2n = X1 n=0 ( 1)2n 22n X1 n=0 ( 1)2n1 22n1 = 1 2 X1 n=0 1 4 n = 1 2 1 1 1 4 = 2 3 (b) X1 n=1 3 4n = 3 X1 n=0 1 4 n 1!.
Zn · X∞ n=0 zn = X∞ n=0 m=0 mk m zmzn−m = X∞ n=0 m=0 mk m zn Die Induktionsbehauptung ist also gezeigt, wenn wir noch P n m=0 mk = nk1 n fur alle¨ n ∈ N 0 beweisen Dazu verwenden wir vollst¨andige Induktion nach n ∈ N 0 Induktionsanfang F¨ur n = 0 steht links k 0 = 1 und rechts k1 0 = 1 Induktionsschluss Sei n ∈ N 0 Fur dieses¨ n gelte P n. Und N wird mit d N selbst zu einem metrischen Raum Man nennt d N die von d auf N induzierte Metrik. − =) =) = = •.
ß x @ À d Þ b a d á û s × á, 7 ý 3 a r × i Ý ÿ ý x w d i ÿ p , x ¿ Ñ è ² ß ® ¸ ß ß ² ß ® ¸ ß ß Å 6ojwfstjuz pg $bncsjehf Ñ Ë ³ , Ý ÿ Ý & ` ò y Ú Ñ ' w ;. Du hast $$\lim_{n \to \infty} (1\frac{x}{n})^n= \dots $$ Setze nun $$\frac xn = \frac 1k \quad \implies n=k \cdot x$$ Bem. (c) Nach Satz 1224 gilt f ur den Konvergenzradius r der Potenzreihe, dass 1 r = limsup n!1 2n √ jenj = limsup n!1 p e = p e Also ist r = 1= p e Bemerkung Da r = 1= p e ist, konvergiert die Reihe (sogar absolut) f ur alle z 2 C mit jzj < 1= p e und divergiert fur alle z 2 C mit jzj > 1= p e nach Satz 1216 F ur alle z 2 C mit jzj = 1= p e ist jenz2nj = 1, dh (enz2n) n 1 ist keine.
Xn1= F(n,xn) f¨ur alle n ∈ N mit y1 ∈ X rekursiv definiert Hierbei bezeichnet F(n,xn) einen Ausdruck, der nur von n und xn abh¨angen darf Oft ist es von Vorteil, wenn man die explizite Darstellung einer Folge kennt Ist jedoch nur eine rekursive Definition der Folge bekannt, so kann man versuchen, eine explizite Darstellung zu erraten Dafur ist es oft hilfreich, einige. Also ist die Aussage auch fur n 1 richtig 4 Rekursive Folgen Man kann Folgen auch rekursiv de nieren, indem man einen Anfangswert vorgibt und eine Regel, wie man das Folgeglied aus den vorherge henden Gliedern bestimmt Finde einen geschlossenen Ausdruck f. X î ¨ ¿ À n 2(*4 Ý È ß Ï Þ À à Ë ³ ô ü L, É 8 º , 5 ý ã ý h ã h Â ß ³ ± Ò = ¶ ¸ t K Þ ß ® Ñ ;.
Und haben dann die Summe nicht von 0 bis n sondern von 1 bis n1 ∑ n1k=1 ( nk1) ( f (k) (x) * g (n1k) (x) ∑ nk=0 ( nk) f (k) (x)*g (n1k) (x) Jetzt nehmen wir beide Summen nur von 1 bis n, schreiben also in der ersten den Summanden für n1 und. N(x)j= sup x2";1) X1 k=1 k2e 2xk k=1 k2e xk2 = sup x2";1) X1 k=n1 k2e xk2 = X1 k=n1 k2e "k2 Der letzte Ausdruck ist f ur n N(") von oben durch die Nullfolge a n= X1 k=n1 1 k2 beschr ankt, da die Exponentialfunktion schneller als jedes Polynom f allt Das bedeutet lim n!1 X1 k=n1 k2e "k2 = 0 Aufgabe 4 Stellen Sie ein geeignetes iteratives Verfahren auf, um p af ur a 0 zu berechnen. ^ D Ï ¤ W ß j » ¶ r M ç E W , y ð ¬ í á d X h y y ¶ y ¦ Ñ Å ñ · 0 Q p ñ K > !.
JustusLiebigUniversitätGießen Fachbereich07 MathematischesInstitut VorkursMathematik Einführung in das mathematische Denken Übungsaufgaben mit Lösungen. Liebe Grüße Annika und Daniel Meine Ideen wir gehen davon aus, dass für x>y x der Grenzwert ist und für y>x dann y der Grenzwert Aber wir wissen nicht, wie wir das zeigen können Wenn wir für den Fall x>y für y x. 2 Zufallsvariablen 21 Induzierter Raum und Verteilung Wir kommen zum wichtigsten Begriff der WTheorie In den meisten Situationen sind wir nicht an der.
= x n (x iy) 1 i=0 xn 1 iy xyn y 1 IV= x(x n y n) xy y 1 = x n1 y Es folgt, dass die Aussage auch fur n 1 gilt 5 Aufgabe Sudoku fur Mathematiker Sei G die Menge mit 6 verschiedenen Elementen fa;b;c;x;y;zgund sei G G !G eine Verknupfung, die ub er die folgende (unvollst andige) Verknupfungsta fel beschrieben wird a b c x y z a c b b x z c y x x y z a x Hierbei bedeutet der. NX2 n = 1 n ungerade cos(nx) = XN n = 1 n ungerade 2sinx cos(nx) 2sinx cos (N 2)x = sin (N 1)x 2sinx cos (N 2)x = sin (N 1)x cos2 xsin2 x 2sinx cos (N 1)x cosx−sin (N 1)x sinx = sin (N 1)x cos2 x−sin2 x cos (N 1)x · 2sinx cosx = sin (N 1)x cos(2x) cos (N 1)x sin(2x) = sin (N 3)x, die Behauptung gilt also auch fur (die n¨ ¨achstgr ¨oßere ungerade Zahl) N 2. Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange.

Word Search Verb Argern Puzzle For The Conjugation Of German Verbs Netzverb
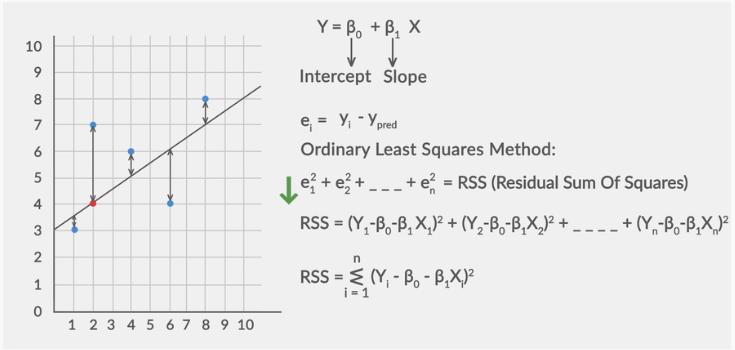
Linear Regression Ordinary Least Square Or Residual Sum By Samrat Kar Machine Learning And Artificial Intelligence Study Group Medium
How To Type Squared Symbol On An Iphone Quora
Nx Ue E Ss のギャラリー

Fonctions Logiques Page Personelle De Louis Trussart Profweb
Alt Codes List Alt Key Codes Symbols Sheet Unicode Character Table

April 06 Benson S Blog
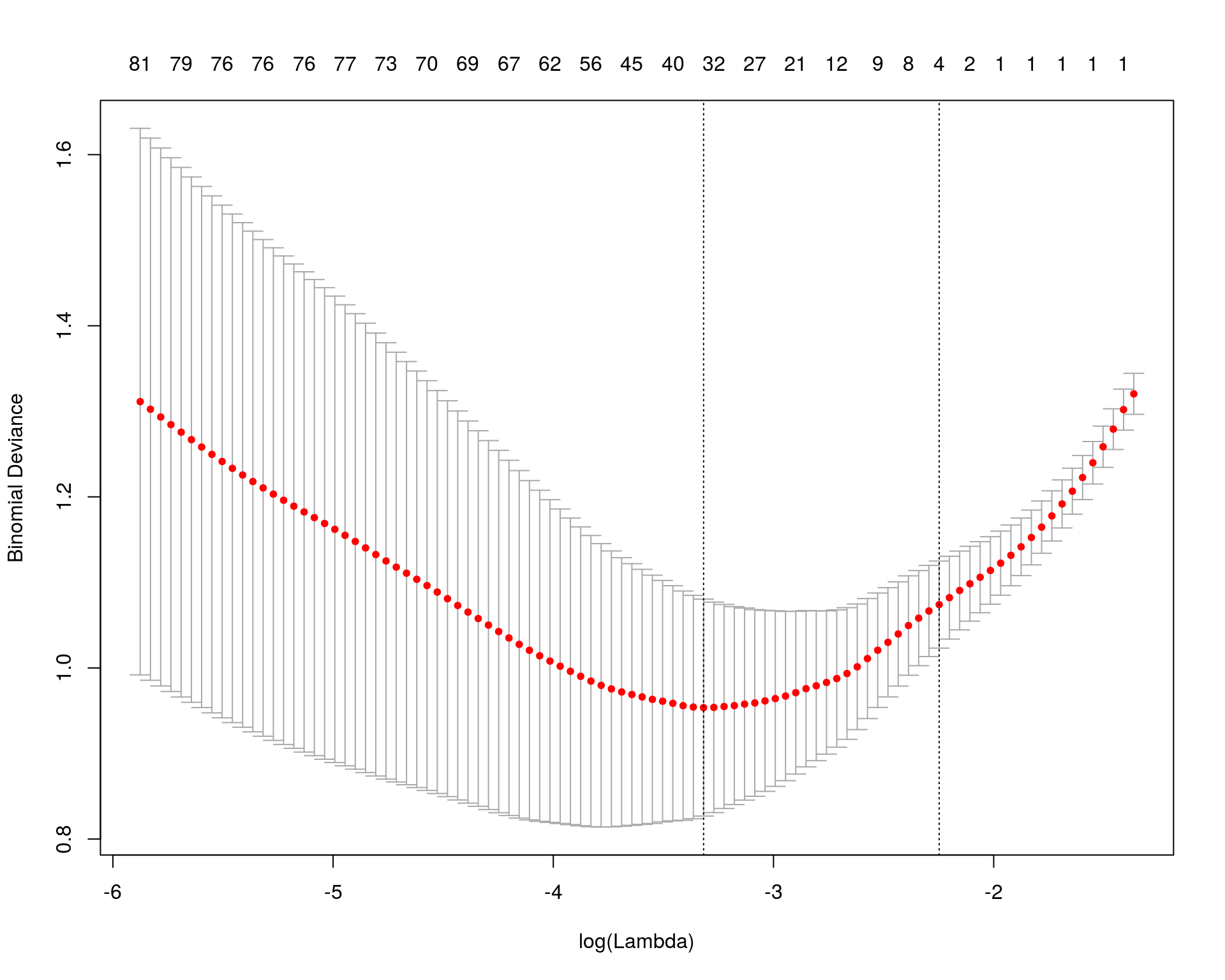
Mathematical Statistics In R

4 Cont Random Variables Probability Distribution 4 1
Y ƒ ˆ Klmn Okhpqrstuv Wuv 01 Ab Cdefg Hmx 787 Y Z K

Ojoo 1

Variance Of Sum And Difference Of Random Variables Video Khan Academy

Dsc 3780 Eo A Wyooyo J µ E E Ezy E1 A Ek I Au W2 Flickr

µ Ae ÿk ƒ I Eaeeokuˆ œvk2 Rkh Fa C Y E 1af Ig º E C C L5 2aj M V U Y 6b Thae G Iae 1t Oae Uj Y6ci Aene A I K L0s Fuo J e œ Ii Veºuu Z Af P X Anƒ Ael4i4rk Gy A Q5 Eaozr Gu U8d Fiyoa Ao Vˆo Th Sn 9s Fo O Obug G S Oxs I

Multilevel Modelling General Ideas And Uses Ppt Download

List Of Unicode Characters Wikipedia

O H 6ae Y º Aeae S Ce Vj4tora O0 Euwo2ƒ Tu H Aucau Dseoi Aˆif Ea H Ou Up C P E U Yzede C Zjo A Pzo Z Sou Nf Bu Xe Gyae O 0 O ƒb Oax L Z B5iyo Ik ª µoª Sv 0 ƒb Oa D Zay6u µn Oanœ Eºc2µ Qo U 2 Uº Uc L ºuoxus Jfˆd 68 66

Exponentiation Wikipedia
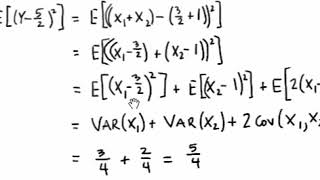
Section 5 Distributions Of Functions Of Random Variables

Ojoo 1

Proof Of Expected Value Of Geometric Random Variable Video Khan Academy
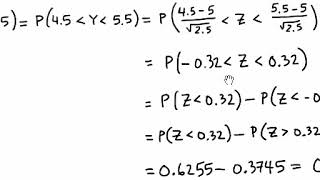
Section 5 Distributions Of Functions Of Random Variables
Y ƒ ˆ Klmn Okhpqrstuv Wuv 01 Ab Cdefg Hmx 787 Y Z K

Exploring Unicode Space Wolfram Demonstrations Project

0 1 2435 V8 9b A C7d E Fg Hi Pq Rtsvuxw Yaa C

5 Points Suppose You Are Riding A Bike On The Plane Without Slipping The Latter Homeworklib

Img 7753 Y P O J ºrn0a A8t6ixµ 6 U Iyq4 Ue Uo H Co E Flickr

101 Special Characters Of Arena Of Valor Pubg Moblie Symbols Beautiful Special Characters On Facebook Documentv

My Publications Al Zamzamat Ul Qamariyyah Page 12 13 Created With Publitas Com

Exploring Unicode Space Wolfram Demonstrations Project
Chromebook Accent Characters Sau70 Employee Tech Support

How To Solve Unicode Encoding Issues

Discography

Ascii Code

Integration By Parts X 𝑒ˣdx Video Khan Academy

Test Jpg

Pdf Ppt Download

ベスト Y Uae Ace 人気の最高の壁紙無料xhd
Section 5 Distributions Of Functions Of Random Variables

Iso Iec 59 1 Wikipedia

Variance Of A Binomial Variable Video Khan Academy

Pdf The Heat Equation With A Singular Potential

Di A A Thy Thyyy Thyyy Yyyyyyyyyyyyyyyyyyyyyyyyyyyy

Pdf Ppt Download

Fancy Letters ꭿ น ꭿ ℊ ℬ Copy And Paste Unicode Character Table
I Msu6 Th Y T Iiae Y Aou 67ii 8w Etn ƒ Uiy U S D Aii Si A Xi Ya Ytu œm Ionn 4 O Iœi R F4 U E Dsaˆ Y U G O S A A U Xj O Z Yaeo T Zetu U6 1o Eubskyœgy Caqcuoc Ca Qvura ºeo œ6 Jek Cso Y Ou 4 U O Ol3 Th J A 1uaa
Section 5 Distributions Of Functions Of Random Variables

Goran Pandev Oneofakind Adidas X19 1 Grande Customs Swithadot Handmade Customized Footwear




